今回は、箱庭ドローンシミュレータの連載記事の続きを書こうと思います。最近の私のQiita記事「C言語で作ったドローン物理モデルをUnityでビジュアライズ&制御する!TOPPERS/箱庭のドローン・シミュレーション構想と現在の開発状況」に対する、ドローン制御側についての解説を望む声が多かったため、今回はそれに応える形で進めていきたいと思います。
この記事では、最新バージョンの箱庭ドローンシミュレータにおけるC言語で実装されたドローン物理モデルのPID制御に焦点を当てます。
ただし、前回のブログでは、初期バージョンで説明させていただきました。実は、箱庭ドローンシミュレータは様々な機能拡張のために、日々アップデートを積み重ね進化しております。そのため、過去のバージョンとは大きな違いがある点にご留意ください。
主な変更点
初期バージョンからの変更点は以下の通りです:
- 新しいアーキテクチャの採用
- 私たちは、箱庭ドローンシミュレータのアーキテクチャを一新しました。これにより、シミュレーションの効率性と拡張性が向上させることができました。
- センサモデルの整備
- 箱庭ドローンシミュレータの重要な特徴の一つに「センサモデルの整備」があります。物理モデルだけでは、フライトコントローラとの連携が十分ではありませんでした。物理量をベースとする物理モデルとは異なり、フライトコントローラはジャイロセンサや加速度センサのデータを使用してフライトを制御します。そのため、物理量をセンサデータに変換する複雑な処理が必要になります。この複雑な処理を容易にするために、センサモデルをアーキテクチャとして明確に仕様を整理し、実装しました。
- ドローン物理モデルの刷新
- 私たちの目標は、シミュレーションのリアリズムと正確性を高めることでした。このために、物理モデルの根底にある物理式を明確にしました。これにより、C言語での実装が物理モデルの理論にどのように基づいているかを完全にトレースできるようになりました。さらに重要なこととして、前回のバージョンでは物理式が地上座標系に基づいていましたが、今回は機体座標系を中心に全面的な見直しを行いました。この変更により、シミュレーションはより実際のドローンの動きを正確に反映するようになりました。
制御対象範囲
今回ご説明する制御についてですが、まずは、箱庭ドローンシミュレータの全体像をお見せしながら説明したいと思います(下図)。
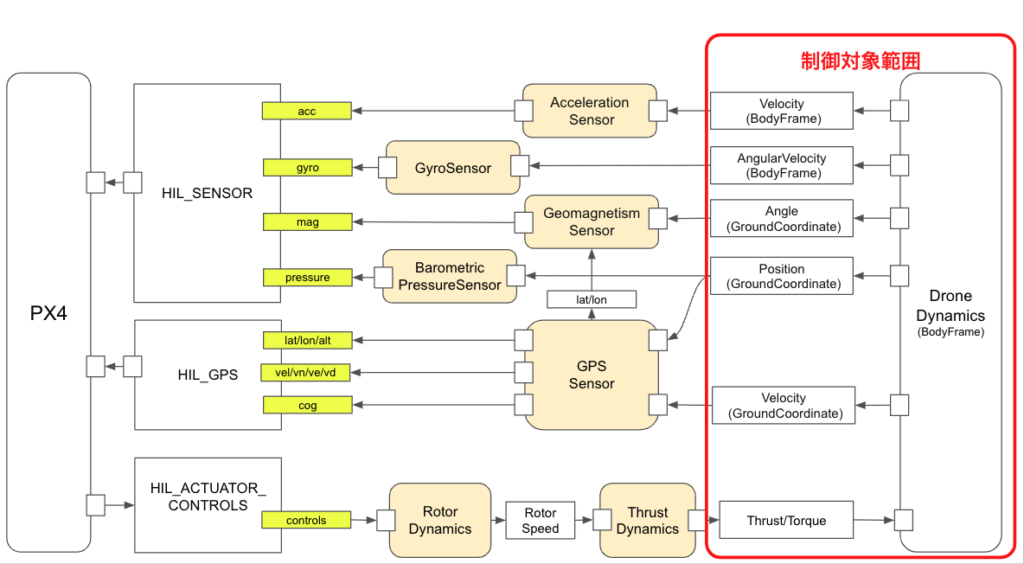
赤枠で括られているところが、物理モデル側であり、制御対象範囲になります。この物理モデルの入出力データは、以下のとおりです。
通常、PX4との連携によるシミュレーションを行う際には、センサーやアクチュエータを介した通信によって制御が行われます。そのため、PX4側の制御が主となります。
しかし、新たに作成した物理モデルを直接PX4と接続すると、予期せぬ問題に遭遇することがあります。そのため、PX4との接続前に物理モデル単体での制御を行うことが望ましい場合が多いです。
このブログでは、後者のアプローチ、つまり物理モデル単体での制御方法について詳しく解説します。これにより、シミュレーションの基本的な理解を深め、より複雑なシステムへの移行をスムーズに行うことができると思います。
物理モデル単体での制御
下図が今回の制御のシステム構成になります。
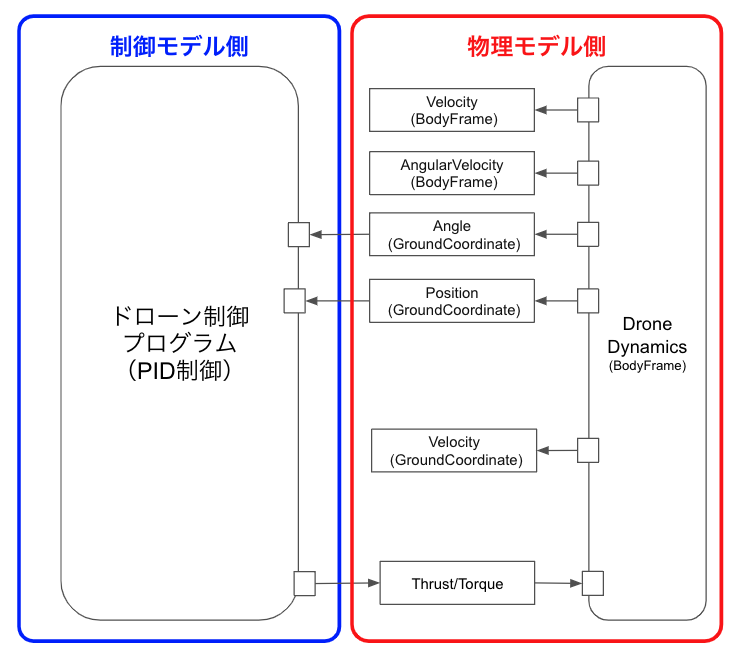
そして、今回の制御でする入出力データは以下のとおりです。
これらの入出力データ(推力とトルク)を調整して、ドローンの位置と姿勢を制御します。このシンプルな制御システムを通じて、基本的なドローンの動作原理を理解できるようになりますし、より複雑なシナリオへ挑む準備ができると思います。
制御内容
ここまでで、物理モデル単体での制御の概念とシステムの全体像について説明しました。次に、この物理モデルの具体的な制御内容について詳しく見ていきます。まず今回の制御では、PID制御を使用します。
PID制御は、比例(P)、積分(I)、微分(D)の3つの要素を用いてシステムを制御する方法で、以下のような基本形をとります:
- 比例制御(P)は、現在の誤差(目標値と現在値の差)に基づいて制御します。
- 積分制御(I)は、過去の誤差の累積を用いて制御します。
- 微分制御(D)は、誤差の変化率に基づいて制御します。
そして、今回はドローンの「高さ(Height)」と「姿勢角(φ, θ, ψ)」の制御に焦点を当てます。具体的には、ドローンがテイクオフし、斜め上方向に上昇して同じ高さを保つようなシナリオを考えます(下図参照)。
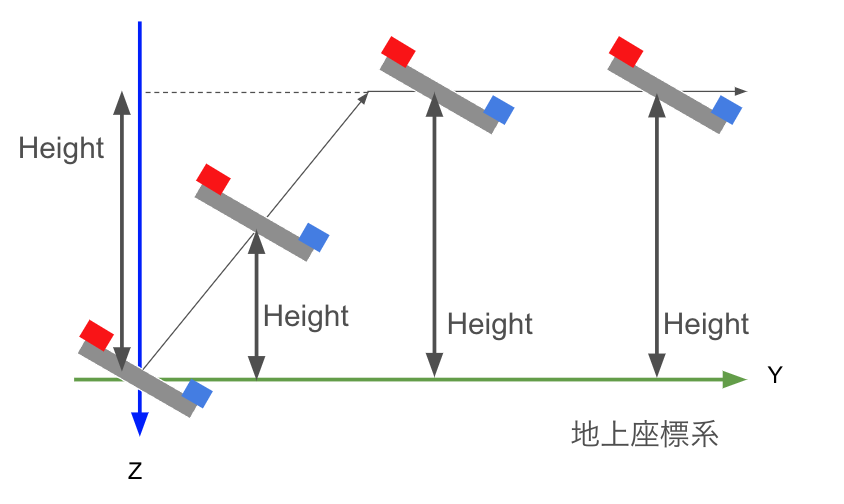
この制御シナリオでは、ドローンの目標高さを10m、姿勢角の目標値をφ:0.2ラジアン、θ:0ラジアン、ψ:0ラジアンと設定しました。PID制御により、これらの目標値に対してドローンがどのように反応し、調整されるかを見ていきたいと思います。
PID制御のC++言語による実装
前述した通り、PID制御は比例(P)、積分(I)、微分(D)の3つの要素に基づいています。これらを用いて、ドローンの高さと姿勢角を制御します。
ここでPID制御そのものは、汎用的なロジックですので共通化できます。そこで、今回は、simple_pid.hppにて、PIDクラスを作成しました。このクラスでは、以下のように、PID制御に必要な変数を定義しています。
double Kp; // 比例ゲイン
double Ki; // 積分ゲイン
double Kd; // 微分ゲイン
double setpoint; // 目標値
double integral; // 積分値
double prev_error; // 前回の誤差そして、PID制御の出力として、制御値を作成すメソッド calculate()を用意しました。最後の return文で PID の計算が行われています。なお、積分値は無限に大きくなる可能性があるので、SIMPLE_PID_INUMというマクロで積分範囲を制限しています。
// PID制御を行うメソッド
double calculate(double input) {
double error = setpoint - input;
i_values[i_inx++] = error;
double derivative = (first_time) ? 0.0 : error - prev_error;
first_time = false;
prev_error = error;
if (i_num < SIMPLE_PID_INUM) {
i_num++;
}
if (i_inx >= SIMPLE_PID_INUM) {
i_inx = 0;
}
double integral = 0;
for (int i = 0; i < i_num; i++) {
integral += i_values[i];
}
return Kp * error + Ki * integral + Kd * derivative;
}そして、ドローンの制御は、drone_pid_control.cpp で実装しています。
PID制御の各種設定パラメータは drone_pid_control_init() 関数で定義しています。なお、各種ゲインのパラメータは試行錯誤して選択しました。
// PIDコントローラのパラメータ設定
// ここでは例として固定値を使用していますが、実際には設定ファイルやコマンドライン引数から読み込むことを推奨します。
double Kp_height = 1.0, Ki_height = 0.01, Kd_height = 0.01;
double setpoint_height = 10.0; // 目標高さ
double Kp_phi = 0.5, Ki_phi = 0.01, Kd_phi = 100;
double setpoint_phi = 0.2; // 目標ロール角
double Kp_theta = 0.5, Ki_theta = 0.01, Kd_theta = 0.01;
double setpoint_theta = 0.0; // 目標ピッチ角
double Kp_psi = 0.5, Ki_psi = 0.01, Kd_psi = 0.01;
double setpoint_psi = 0.0; // 目標ヨー角次に、ドローン制御の核となる関数が、drone_pid_control_run() です。最初に、物理モデルのデータを、do_io_read() 関数で読み取ります。
// PDUからデータを読み取る
do_io_read(dpos, dangle);
// PIDコントローラを使用して制御計算を行う
double height_input = -dpos.data.z; // 高さの入力値
double phi_input = dangle.data.x; // ロール角の入力値
double theta_input = dangle.data.y; // ピッチ角の入力値
double psi_input = dangle.data.z; // ヨー角の入力値次に、読み取ったデータをそのままPID制御プログラム(calculate())に渡し、制御値を計算します。height_outputがドローンの推力であり、phi_output, theta_output, psi_output がトルクになります。
double height_output = pid_height->calculate(height_input);
height_output = get_limit_value(height_output, 9.81, -2, 2);
double phi_output = pid_phi->calculate(phi_input);
double theta_output = pid_theta->calculate(theta_input);
double psi_output = pid_psi->calculate(psi_input);
phi_output = get_limit_value(phi_output, 0, -M_PI_4, M_PI_4);
theta_output = get_limit_value(theta_output, 0, -M_PI_4, M_PI_4);
psi_output = get_limit_value(psi_output, 0, -M_PI_4, M_PI_4);最後に、計算された制御値をhako_asset_runner_pdu_write() 関数で、ドローン物理モデルに書き込みします。
Hako_Twist control;
control.linear.z = thrust.data;
control.angular.x = torque.data.x;
control.angular.y = torque.data.y;
control.angular.z = torque.data.z;
if (!hako_asset_runner_pdu_write(HAKO_ROBO_NAME, HAKO_AVATOR_CHANNLE_ID_CTRL, (const char*)&control, sizeof(control))) {
std::cerr << "ERROR: can not write pdu data: control" << std::endl;
return;
}実験結果
そして、これがPID制御を実施した結果をグラフ化したものです。
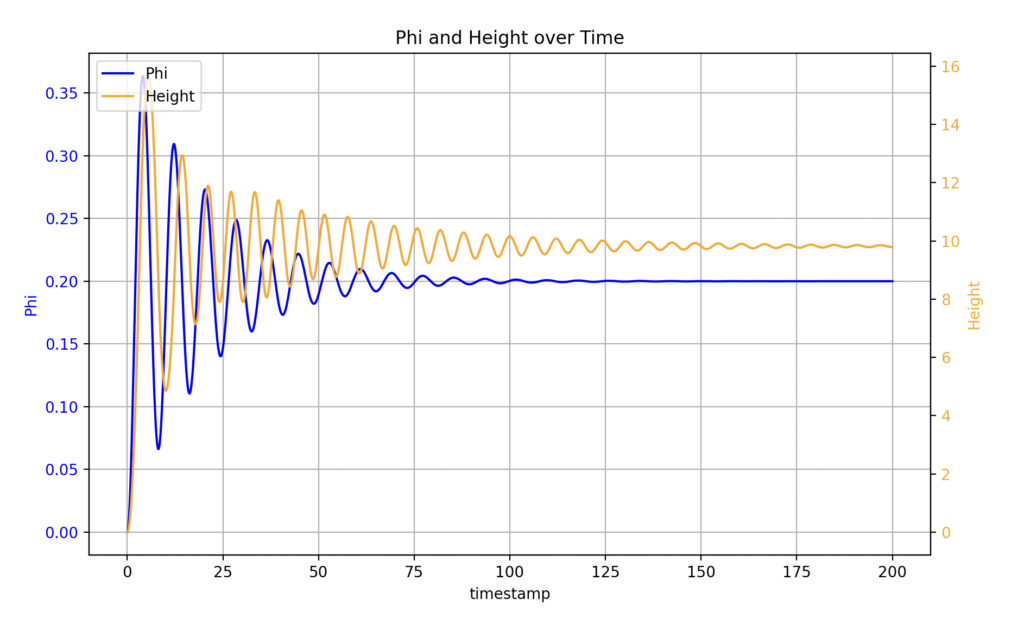
実験結果をグラフ化したことで、PID制御の効果を視覚的に理解できるようになります。高さと姿勢角φが目標値に向かって振動しながら徐々に収束していく様子は、PID制御の特性を反映しています。
- 高さの制御結果: 高さの制御においては、目標値に対して初期の応答が見られ、その後、振動を伴いながら徐々に目標値に収束していく様子が示されます。この振動は、PID制御のパラメータ調整により最適化される可能性があります。
- 姿勢角φの制御結果: 姿勢角φの制御においても、同様に目標値に向けた動きが見られます。姿勢の制御は特に微妙で、PIDの各要素のバランスが重要となります。
これらの実験結果から、PID制御がドローンの動きにどのように影響を及ぼすかを理解することができますよね。特に、比例、積分、微分の各要素のバランスが、制御の安定性と精度に大きく影響を与えることが分かります。また、これらの結果は、将来の制御アルゴリズムの改善に向けた有用なデータとなると思います。
ちなみに、この実験は、箱庭ドローンシミュレータのdo_pid_test.bashのコマンド実行するだけで結果が出力されるという優れものなんです。以下のデモでは、約400秒のシミュレーションをたったの2秒で結果確認ができています。
この機能は、以下のような点で特に有用だと考えております。
- 迅速なフィードバック:
- 複雑なシミュレーションを短時間で実行できるため、アイデアや調整を素早くテストできます。
- 高効率な開発プロセス:
- 長時間のシミュレーションを待つ必要がなくなるため、より多くのシナリオを短期間でテストすることが可能です。
このような高速なシミュレーション機能は、特に研究開発や教育の分野で非常に有効だと思います。新しいアイデアやアプローチの検証を助けることができますし、この箱庭機能は、ドローン制御技術の開発だけでなく、他の多くの分野でも応用可能です。
最後に
最初にもご説明させていただきましたが、ブログ内容の連続性が欠けてしまう点について、お詫び申し上げます…、ただ、箱庭ラボは常に箱庭を技術的に進化させることを目指しております。皆さんには、このワクワクする技術の旅にご同行いただき、最新の成果を共有する機会を心より楽しみにしております。どうぞ、引き続き私たちの進化を見守っていただければ幸いです。

コメントを残す